Fritz John conditions
The Fritz John conditions (abbr. FJ conditions), in mathematics, are a necessary condition for a solution in nonlinear programming to be optimal. They are used as lemma in the proof of the Karush–Kuhn–Tucker conditions.
We consider the following optimization problem:
where ƒ is the function to be minimized, 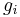 the inequality constraints and
the inequality constraints and 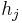 the equality constraints, and where, respectively,
the equality constraints, and where, respectively, 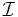 ,
, 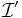 and
and 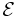 are the indices set of inactive, active and equality constraints and
are the indices set of inactive, active and equality constraints and 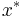 is a optimal solution of
is a optimal solution of  , then there exists a non-zero number
, then there exists a non-zero number 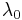 and a non-zero vector
and a non-zero vector ![\lambda=[\lambda _1, \lambda _2,\dots,\lambda _n]](/2012-wikipedia_en_all_nopic_01_2012/I/9e59dd07e7c364ad714711c840cf0a6e.png) such that:
such that:
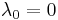 iff the
iff the 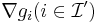 and
and 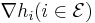 are linearly dependent and
are linearly dependent and 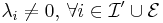 , i.e. if the constraint qualifications do not hold.
, i.e. if the constraint qualifications do not hold.
Named after Fritz John, these conditions are equivalent to the Karush–Kuhn–Tucker conditions in the case 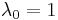 .
.
References
- WANG Yiju, XIU Naihua (in Chinese). 非线性规划的理论和方法 (The theory and methods of the Non-linear programming). p. 4. ISBN 9787536938250.
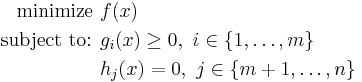
![\begin{cases}
\lambda_0 \nabla f(x^*) = \sum\limits_{i\in \mathcal{I}'} \lambda_i \nabla g_i(x^*) %2B \sum\limits_{i\in \mathcal{E}} \lambda_i \nabla h_i (x^*) \\[10pt]
\lambda_i \ge 0,\ i\in \mathcal{I}' \\[10pt]
\exists i\in \left( \{0,1,\ldots ,n\} \backslash \mathcal{I} \right) \left( \lambda_i \ne 0 \right)
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/56594576c6984b4d746fbd6a1738e788.png)